Introducción a la Computación Cuántica con Qiskit

La computación cuántica es un campo fascinante que promete revolucionar el procesamiento de la información al aprovechar los principios de la mecánica cuántica. En este blog, exploraremos los conceptos básicos, implementaremos un circuito cuántico con Qiskit , y mencionaremos acerca de Majorana , una de las tecnologías más prometedoras en este campo.

Conceptos Básicos

Antes de sumergirnos en el código, es importante comprender algunos términos clave:

• Qubit : Unidad básica de información cuántica, que puede estar en estado $|0\rangle$, $|1\rangle$ o en una superposición de ambos, representada matemáticamente como:

  $∣ψ⟩=α∣0⟩+β∣1⟩$

  donde $\alpha$ y $\beta$ son números complejos que cumplen $|\alpha|^2 + |\beta|^2 = 1$.

• Superposición : Propiedad que permite que un qubit exista en múltiples estados simultáneamente. Esta propiedad fundamental de la mecánica cuántica permite que los qubits representen y procesen muchos valores a la vez.

• Entrelazamiento : Conexión cuántica entre qubits, donde el estado de uno afecta instantáneamente al otro, sin importar la distancia. Un estado entrelazado de dos qubits puede representarse como:

  $\|\psi\rangle = \frac{1}{\sqrt{2}} (|00\rangle + |11\rangle)$

  Este es uno de los estados Bell, donde medir un qubit determina instantáneamente el valor del otro.

• Puerta Hadamard (H) : Operación que coloca un qubit en superposición. Su representación matricial es:

  $H = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}$

  Aplicada a $|0\rangle$, produce $\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)$.

• Puerta CNOT : Operación que entrelaza dos qubits, donde el estado del segundo qubit (target) se invierte si el primer qubit (control) está en estado $|1\rangle$. Su matriz es:

  $CNOT = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix}$

• Medición : Acción de observar un qubit, lo que colapsa su estado cuántico según las probabilidades $|\alpha|^2$ para $|0\rangle$ y $|\beta|^2$ para $|1\rangle$.

---

Creando un Circuito Cuántico con Qiskit

En este apartado, implementaremos un circuito cuántico básico utilizando Qiskit , el framework de código abierto desarrollado por IBM para la computación cuántica.

Paso 1: Importar las Bibliotecas Necesarias

from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit

Importamos los módulos esenciales de Qiskit para crear y manipular circuitos cuánticos:

• QuantumRegister: Para definir los qubits del circuito
• ClassicalRegister: Para almacenar los resultados de las mediciones
• QuantumCircuit: Para construir el circuito cuántico con las operaciones deseadas

Paso 2: Crear un Qubit en Superposición

qr_atom = QuantumRegister(1, name="atom")
qc = QuantumCircuit(qr_atom)
qc.h(qr_atom[0])
qc.draw("mpl")

• Se crea un registro cuántico con un qubit llamado atom.
• Se aplica una puerta Hadamard (H) , transformando el estado inicial $|0\rangle$ en una superposición:

• qc.draw("mpl") visualiza el circuito usando Matplotlib, mostrando la aplicación de la puerta H.

Paso 3: Medir el Qubit

cr = ClassicalRegister(1, name="result")
qc.add_register(cr)
qc.measure(qr_atom, cr)

from qiskit_aer import AerSimulator
backend = AerSimulator()
result = backend.run(qc).result()
print(result.get_counts())

• Se agrega un registro clásico para almacenar los resultados de la medición.
• Se mide el estado del qubit, colapsando la superposición.
• Se ejecuta en un simulador cuántico AerSimulator.
• result.get_counts() muestra la distribución de resultados (aproximadamente 50% de 0 y 50% de 1), siguiendo la probabilidad:

Paso 4: Crear un Estado Entrelazado (Bell)

qr_atom = QuantumRegister(1, name="atom")
qr_cat = QuantumRegister(1, name="cat")
qc = QuantumCircuit(qr_atom, qr_cat)
qc.h(qr_atom[0])
qc.cx(qr_atom[0], qr_cat[0])
qc.draw("mpl")

• Se definen dos qubits: atom y cat.
• Se coloca el qubit atom en superposición mediante la puerta Hadamard.
• Se aplica una puerta CNOT (representada por cx), utilizando atom como control y cat como objetivo.
• Esto genera un estado entrelazado Bell :

En este estado, si medimos uno de los qubits y obtenemos 0, el otro qubit también será 0; si obtenemos 1, el otro qubit también será 1.

Paso 5: Medir y Ejecutar

cr_atom = ClassicalRegister(1, name="c_atom")
cr_cat = ClassicalRegister(1, name="c_cat")
qc.add_register(cr_atom, cr_cat)
qc.measure(qr_atom, cr_atom)
qc.measure(qr_cat, cr_cat)

result = backend.run(qc).result()
print(result.get_counts())

• Se agregan registros clásicos para almacenar los resultados de las mediciones de ambos qubits.
• Se mide el circuito y se ejecuta en el simulador.
• Los resultados mostrarán aproximadamente 50% de 00 y 50% de 11, demostrando el entrelazamiento cuántico.

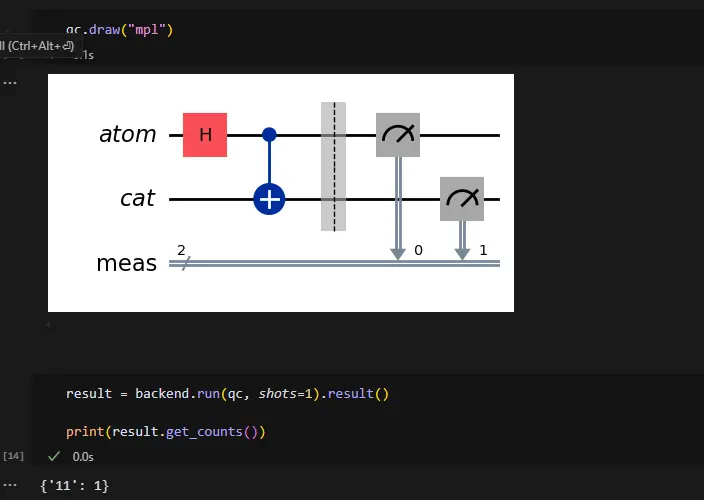
Al ejecutar obtuve ‘11’: 1 en este universo, el gato murió.

---

¿Qué es el chip de Majorana?

El chip de Majorana es un dispositivo experimental presentado el 19 de febrero, diseñado para albergar fermiones de Majorana, partículas teóricas que actúan como su propia antipartícula. Estas partículas tienen aplicaciones prometedoras en la computación cuántica, ya que podrían permitir la creación de qubits topológicos, que son más resistentes a los errores que los qubits convencionales.

Diferencias entre IBM y Majorana

Ventajas de los Qubits de Majorana

• Menos errores: Son más estables gracias a su naturaleza topológica.
• Escalabilidad: Permiten una computación cuántica más eficiente.
• Resistencia al ruido: Reducen la necesidad de corrección de errores.

Si se logran demostrar y controlar los fermiones de Majorana en estos chips, podrían dar lugar a computadoras cuánticas más estables y escalables, superando las limitaciones de los sistemas actuales.

---

Si te gusta el contenido o tienes dudas/sugerencias escríbeme a @josephsilva_21